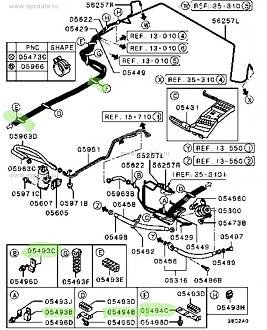
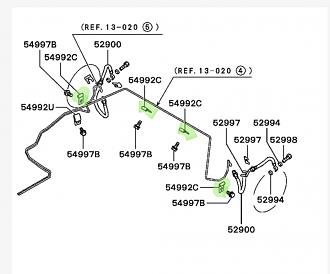
Ordered some guide coat spray and will use it over straight and continuous curves such as the arches. there's a lot of curves around the suspension turrets and I cant see how I could sand these properly so will just try to take the edge off them.If you want, you could blow a bit of guide coat over it to show up any problem areas before the final sanding and sealing coats.
Bit OTT for an engine bay but good practice for you.
You will be surprised what guide coat will show up.
Any tips to prevent the sandpaper from gumming up?