- Forums
- Tools, Compressors and Metal Coatings
- Tools, Materials and Techniques
- Machining
- Lathes and other Machining Equipment
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
New to me - Colchester Triumph
- Thread starter Lewis_RX8
- Start date
Kram
Member
- Messages
- 8,418
- Location
- Sussex
Its splash oil lubed/cooled so I'd expect it to run cooler.
Check if theres any hot spots inside after running. Run on high without cutting to see what the vfd shows for power use.
It gets heat moving from the work to the spindle but that would take a while of heavy cutting.
Check if theres any hot spots inside after running. Run on high without cutting to see what the vfd shows for power use.
It gets heat moving from the work to the spindle but that would take a while of heavy cutting.
Lewis_RX8
Member
- Messages
- 1,556
- Location
- Scotland
Cheers folks , I will check the bearing preload but just wanted to know if it was just mine that was wrong rather than trying to fix a non issue.
@minimutly Thinking might release the preload seems the obvious place to start as heat zone is for sure the tapered roller bearings, seems to spin alright and is free enough
@Kram Pretty sure I narrowed the heat down to the bearing areas but worth double checking and not sure if the power usage will be accurate enough from what i can measure but worth a look.
@minimutly Thinking might release the preload seems the obvious place to start as heat zone is for sure the tapered roller bearings, seems to spin alright and is free enough
@Kram Pretty sure I narrowed the heat down to the bearing areas but worth double checking and not sure if the power usage will be accurate enough from what i can measure but worth a look.
Lewis_RX8
Member
- Messages
- 1,556
- Location
- Scotland
Lathe roughly leveled up with some torpedo levels to get.it close enough for when I get @winchboy 's level delivered to get a precise level on it
Now trying to get the lathe headstock aligned close in will have to finalise once I have the accurate level again but it is 0.3mm out so that's definitely not all down to a little bit out of level so will need to fiddle with the alignment bolts , reading 50.08 at chuck end and 50.41 at tailstock end and that's over 15cm about 6"

He had never touched the headstock cover so Sharpie marks must have been from RAF base days over 20 years ago ! , He ran the lathe quite a bit the odd day and says it was fine for him and he would't consider the 40°c a problem and has been fine for his use so
Now trying to get the lathe headstock aligned close in will have to finalise once I have the accurate level again but it is 0.3mm out so that's definitely not all down to a little bit out of level so will need to fiddle with the alignment bolts , reading 50.08 at chuck end and 50.41 at tailstock end and that's over 15cm about 6"
Ask the original owner he is a really decent chap.
He had never touched the headstock cover so Sharpie marks must have been from RAF base days over 20 years ago ! , He ran the lathe quite a bit the odd day and says it was fine for him and he would't consider the 40°c a problem and has been fine for his use so
Lewis_RX8
Member
- Messages
- 1,556
- Location
- Scotland
Don't turn the whole bar make it like a dumb bell. Turn down in the centre then leave a collar each end.
Just machine the collars. Say an inch wide each end.
Ah okay did not think about that , will do it that way next cut
Also is there any technique for knowing how to adjust for the readings I get and which way the taper goes or should I get adjust some bolts and see if they decrease or increase taper then do what works.
Pete.
Member
- Messages
- 14,999
- Location
- Kent, UK
Big at free end - headstock needs to come towards you.
Big at chuck end - headstock needs to go away from you.
Hasn't this lathe got a Vee for headstock alignment? Surely it doesn't have jacking bolts as well?
Colchesters usually have a dowel front left and jacking bolts at the rear to turn the headstock.
Lewis_RX8
Member
- Messages
- 1,556
- Location
- Scotland
@Munkul A photo of it on a pallet I will get better ones when I am back out , these are used to push it either way then use the locking nut to hold.it I believe
I have seen these bolts with lock nut that I think pivots the headstock around aswell as some Alan heads which hold the headstock to the bed that you need to loosen off to pivot

I have seen these bolts with lock nut that I think pivots the headstock around aswell as some Alan heads which hold the headstock to the bed that you need to loosen off to pivot
Hood
Member
- Messages
- 17,542
- Location
- Carnoustie, Scotland
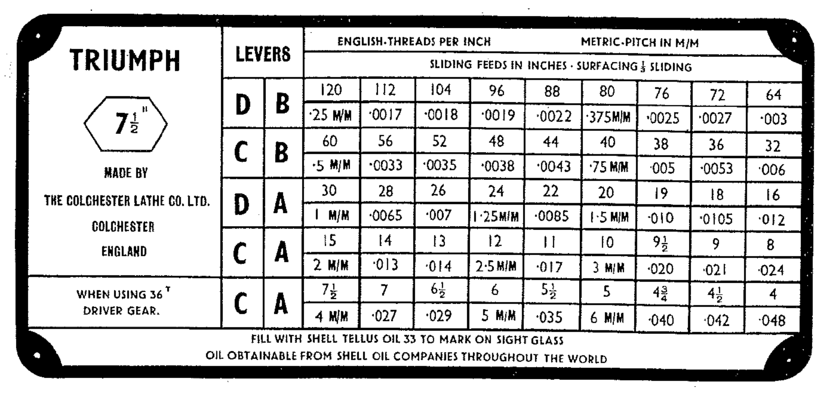
If I recall there is also a lever that switches between metric and imperial so it probably does make sense.I cant make sense of that. 1mm is not 30 thou and 7.5 thou is not 4mm.
The 30 in your example is likely TPI.