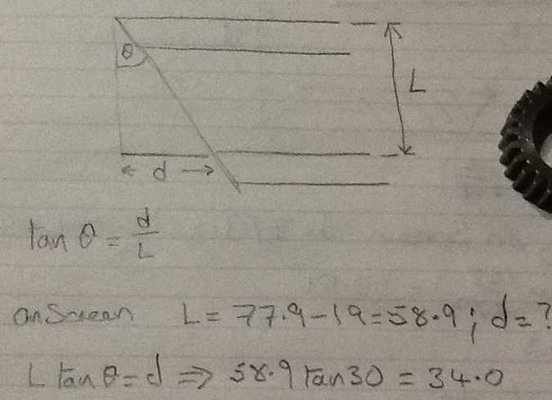- Thread starter mart
- Start date
Screwdriver
Member
- Messages
- 10,675
Looks like you have used my calculated 77.9mm instead of the given dimensions in the original "problem".
Length of wooden "supports" 284mm and 250mm respectively, therefore "d" in your example is given as 34mm.
Desired angle is given as 30˚. You should end up with this:
Immediately you can see the (new) problem. The given dimensions calculate the "run" minus the thickness of the support, assuming "run" means to include that dimension.
What we know is that the run calculated at 58.9mm needs 19mm added to account for the thickness of the wood. This gives us a new triangle as below.
So in summary, this "simple" example which "proves" you should use maths to solve the problem, really proves you probably shouldn't!
Me? I'm going to stick to Sketchup...
Length of wooden "supports" 284mm and 250mm respectively, therefore "d" in your example is given as 34mm.
Desired angle is given as 30˚. You should end up with this:
Immediately you can see the (new) problem. The given dimensions calculate the "run" minus the thickness of the support, assuming "run" means to include that dimension.
What we know is that the run calculated at 58.9mm needs 19mm added to account for the thickness of the wood. This gives us a new triangle as below.
So in summary, this "simple" example which "proves" you should use maths to solve the problem, really proves you probably shouldn't!
Me? I'm going to stick to Sketchup...
roblane65
Member
- Messages
- 2,231
- Location
- Newcastle UK
Get a roofing square it's simple to use for basic roofing set the angle and it gives you the plumb cut and seat cut 
Stanley Adjustable Quick Roofing Square Rafter Saw Guide Protractor Aluminium 76174460537 | eBay
Can be used as a saw guide, protractor, rafter or combination square, with locking adjustable arm for fast, accurate repetition of cuts. Ideal for calculating angles for marking seat and plumb cuts on rafters and joists.
www.ebay.co.uk
MysterG
Member
- Messages
- 1,281
- Location
- Wiltshire, UK
When I was 11 I wrote a program to calculate trigonometry stuff. Got it published in a computer magazine, one of those ones where they printed out the program for you to type into your BBC micro.
Got paid over £100 for it
Wish I'd though to rewrite it as an app when smartphones first came along.
Sorry for the topic deviation
Got paid over £100 for it
Wish I'd though to rewrite it as an app when smartphones first came along.Sorry for the topic deviation
Screwdriver
Member
- Messages
- 10,675
The problem is really not how to calculate angles and dimensions, the problem is more about which angles and dimensions to calculate.
There's no problem using a roofing square to make a roof (!) but the margin for error is gigantic! Luckily wood is very forgiving so in the real world it doesn't matter unless you're a furniture maker or a boat builder.
There's no problem using a roofing square to make a roof (!) but the margin for error is gigantic! Luckily wood is very forgiving so in the real world it doesn't matter unless you're a furniture maker or a boat builder.
roblane65
Member
- Messages
- 2,231
- Location
- Newcastle UK
Its like everything else , all worked out on relying on everything is square level and parallel which in the real world is rare.
which is when years of expierence come in but a roofing squares a good starting point. Although I wouldn't say the margin for error gigantic.
which is when years of expierence come in but a roofing squares a good starting point. Although I wouldn't say the margin for error gigantic.
Screwdriver
Member
- Messages
- 10,675
Not so sure I understand the question let alone the answer
Bob
IKR, it was not a well framed question but the OP was asking for a formula and that is simply to multiply the length you already know by the tangent of the angle you desire.
For 30˚ or 60˚ (and certainly 45˚) the calculations are trivially easy.
Tan opposite/adjacent (TOA)
Sin opposite/hypotenuse (SOH)
Cos opposite/hypotenuse (COH)
The 'difficult" bit is deciding where those measurements should be made and if you need tan, cos or sin.
Screwdriver
Member
- Messages
- 10,675
I only say that in the context of working out your "run and rise" if for example you just want to know how big your shed roof needs to be to fit or how to fit a shed under a given length of roof panels. I appreciate you can mark out a 4x2 with a negligible margin of error but not if you project that angle the entire span of a roof. In reality it doesn't really matter of course because you just make it fit and the "exact" pitch of the roof does not usually need to be particularly accurate.
eLuSiVeMiTe
Member
- Messages
- 16,441
- Location
- ......
I use a run rise calc or mark up on the wall.
Mark up and cut one joist
Test and adjust
As long as I'm square and parallel I use that as a template for every other rafter.
Screwdriver
Member
- Messages
- 10,675
Does the run and rise calculator take account of the thickness of the material?
Have you got an example rr calculator to have a look at?
Have you got an example rr calculator to have a look at?
eLuSiVeMiTe
Member
- Messages
- 16,441
- Location
- ......
Rafter Calculator - Metric
Calculate all rafter dimensions and cut angles to frame a roof - Metric
www.blocklayer.com
Would be the more involved.
Or something simple like that and adjust yourself for timber/overhang etc.
Rise in Run Pitch Angle Grade - Metric
Calculate rise pitch angle and grade from entered run with animated scaled diagram - Metric
www.blocklayer.com
roblane65
Member
- Messages
- 2,231
- Location
- Newcastle UK
similar here usually test the template at both ends gives a good idea if anything is wildly out.
Screwdriver
Member
- Messages
- 10,675
Rafter Calculator - Metric
Calculate all rafter dimensions and cut angles to frame a roof - Metric
Would be the more involved.
Or something simple like that and adjust yourself for timber/overhang etc.
Rise in Run Pitch Angle Grade - Metric
Calculate rise pitch angle and grade from entered run with animated scaled diagram - Metric
OK that does look handy. As close to CAD as makes no difference! I guess that would be useful to have on your mobile.
I still like to have a plan and Sketchup does that for me. I generally "need" to see it because otherwise I'm going to forget that "plumb cut setback" and cut everything too short!
Ah, school maths lessons . . . "but Sir, no-one needs to know this . . . "
Deciding which to use is easy, as taught to us back in 1983/4 ish by Mr Mason, a London Chelsea supporter, teaching in a school in Yorkshire . . .
Some Old Hag (Sin = opposite / hypotenuse SOH)
Cracked All Her (Cos = opposite / hypotenuse (COH)
Teeth On Asparagus (Tan opposite / adjacent (TOA)
Luckily, by then we were allowed to use calculators, rather than having to look up tables. Prior to super duper 3D CAD and sheet metal applications that generate flat patterns that are sometimes of use, our sheet metal lads used to be impressively good at working such things out - a lot better than me!
MattF
Forum Supporter
- Messages
- 17,352
- Location
- South Yorkshire
Go on you know you want to
I've resisted this long. I'm not giving in yet.
I would say it's "hard" to resist, but that'd just make it worse. 
graffian
Seer unto the end of his beard
- Messages
- 3,781
- Location
- gatwick
The formulas are pretty simple and have been mentioned a few times above.
Draw it out and see what you know and what you want to know.
I ignored the thickness of the wood, I expected the cutting/marking from the same face, either the top or bottom face.
The total thickness/height would be what I used as the adjacent+the lower thickness of wood.
Always beware the missing wedge and complementry angles[30º + 60º].
I learned all this a long time and ago and even with my wonderfull memory can remember opp/hyp, adj/hyp, opp/adj.
